Lec 10 - RREF and Rank

Wednesday, January 25, 2012

2:16 AM

Recall:

 

A system of linear equations is homogeneous if the RHS contains only zeros.



 

Eg

The only solution of









 

 

 

We know





Thus the set is linearly independent.

 

Eg.

Solve







 





 



 







 

The solution set has vector equation



 





 

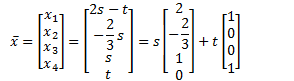
 Theorem:



 

Rank

 

Definition

The rank of a matrix is the number of leading ones in the RREF of the matrix.

 



 

Eg.



 



 

 Theorem



 

1. 

 

2. 

 

3. 

 

Proof:

 



 

1. 

 

2. 





 

3. 





 

Eg.



 

First, is the set linear independent?









 







 



 

 

 

 Proof



 

Note that every homogeneous system is consistent.



 

If there is an infinite number of solutions, let



…



Be the homogeneous system.

 

Apply the Subspace Test:

The solution set is non-empty since the system is consistent.